
August 10, 2020
Along with unsupervised and supervised learning, another area of machine learning is reinforcement learning. Reinforcement learning is concerned with how software agents should take actions in an environment in order to maximize the notion of cumulative reward. Many fields such as game theory, control theory, and statistics use ideas based on reinforcement learning where researchers are more interested in finding the existence of optimal solutions, and algorithms for their exact computation, and less with learning or approximation. In this article, I will go through my exploration with reinforcement learning using a Markov decision process in creating an agent to learn the game of Tic Tac Toe.

A Markov decision process (MPD) uses the ideas from a Markov chain where it’s a mathematical system that experiences transitions from one state to another according to certain probabilistic rules. The Markov chain takes the probabilities associated with various state changes are called transition probabilities. The process is characterized with a transition matrix describing the probabilities of particular transitions and an initial state or distribution. It is assumed that all possible states and transitions have been included in the definition of the process, so there is always a next state, and the process does not terminate. Markov chains can appear as a random walk in thermodynamics or the statistical example of Gambler’s Ruin. More on gambler’s ruin here, and random walks here.
When we define reinforcement learning and the Markov decision process, it is not surprising to see the parallels and how Markov processes fall in place. Reinforcement learning has four main concepts: Agent, Enviroment, Action, and Rewards. The agent refers to the program you train, with the aim of doing a job you specify. Environment: the world, real or virtual, in which the agent performs actions. Action: a move made by the agent, which causes a status change in the environment. Rewards: the evaluation of an action, which can be positive or negative. The process can be outlined in the figure below.
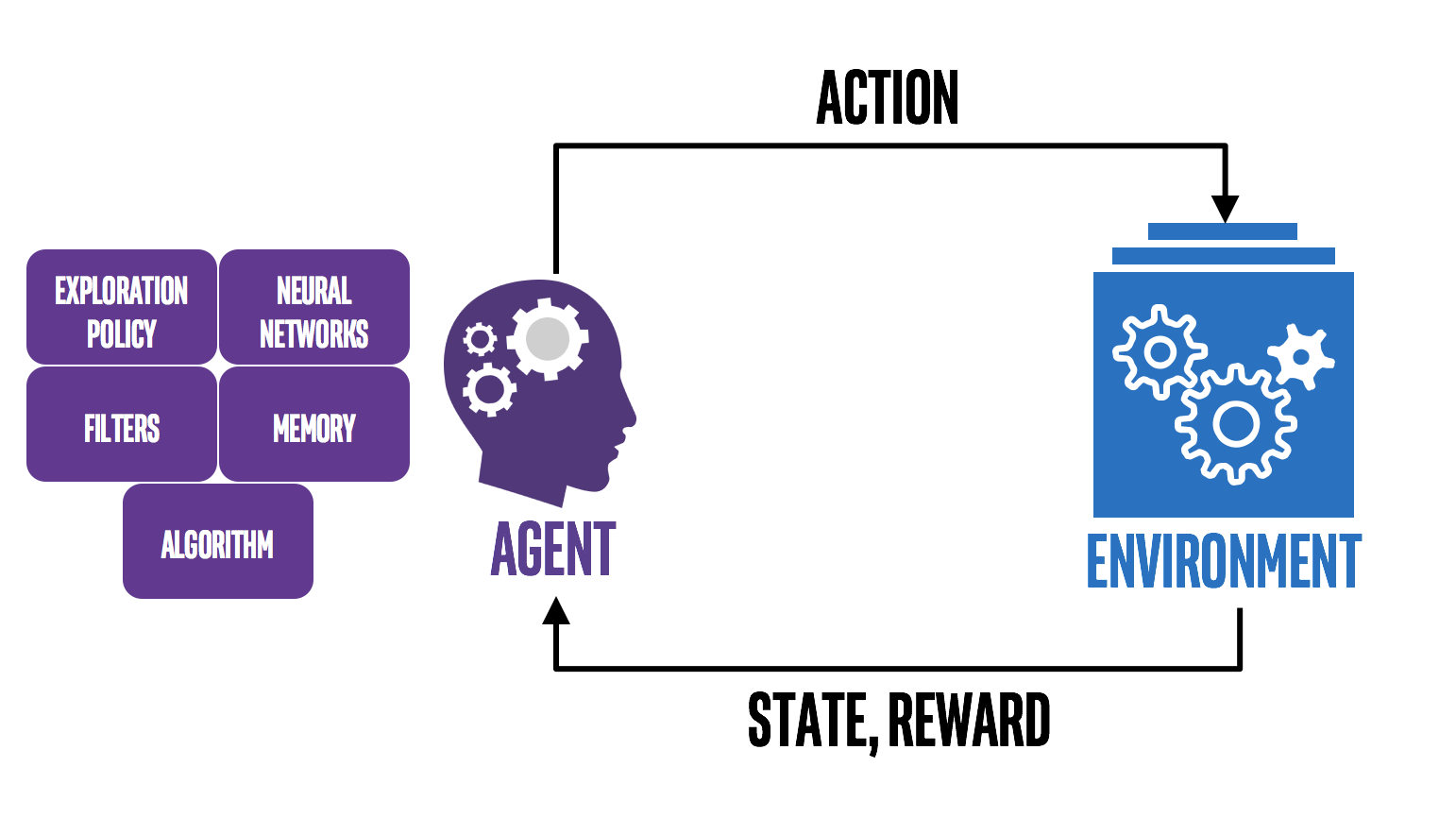
The Markov decision process differs from the Markov Chain in that it uses these “actions” we defined above: a move made by the agent, which causes a status change in the environment. This implies that the next state is related to the actions taken in the current state rather than the basic current state. Also, unlike the Markov chain, the MPD can lead to rewards. The whole goal is to use the MPD to return the maximum number of rewards, essentially the agent learns by getting a “reward” for making the correct decision. For more about the statistics and theory behind MDP, there's a nice paper I found from Rice University.
With all that in mind, time to design a model to learn the game of Tic Tac Toe (TTT). Theoretically, the agent will be optimized when it receives a draw every time during training. TTT is one of those games where if each player is playing the ideal move, then the game will end in a draw. First, I made a class that generates a tic tac toe board. This can be done by creating an n-dimensional array and populating it with all zeros with the “np.zeros” function in numpy. A written function is made to generate and reset the board.
class Board:
# creation of a class to generate the shape of the board, 3x3
def __init__(self):
self.np = __import__('numpy')
self.board = self.np.zeros(9).reshape(3,3) # use numpy to create a new array of given shape filled with zeros.
def reset(self):
self.board = self.np.zeros(9).reshape(3,3)
Other funtions were created under the Board class which tracked the placements of the players, and to act as a form of evaluation. Next, a class was created to act as a computer player, where it made the move, anfd tracked and stored the moves. A TTT class is made that simulates the games between both Computer versus Computer, and gives the option for Player versus the Computer. The code is found on the Github repository. In a seperate file, the training and playing of the game takes place.
def train(cold=True, name='data.csv', n=10000):
# trains computer and saves data, is adjusted for both cold and warm starts when applicable.
ttt = TicTacToe.TicTacToe()
if cold:
print('Stochastic\n')
wins1 = ttt.CvC(iterations=int(0.2*n), rand=True)
print('Learning\n')
wins2 = ttt.CvC(iterations=int(0.8*n), rand=False)
ttt.comp.store_dta(name)
wins = wins1.append(wins2, ignore_index=True)
x = wins.groupby(wins.index//100).sum()
plt.plot(x['win'])
plt.show()
else:
print('Loading...')
ttt.comp.load_dta(name)
wins = ttt.CvC(iterations=n, rand=False)
ttt.comp.store_dta(name)
x = wins.groupby(wins.index//100).sum()
plt.plot(x['win'][:-1])
plt.show()
The data.csv file saves the moves which can be uploaded into a function that allows to be user to play tic tac toe. The computer uses the data trained on the Computer versus Computer to determine its moves. It did a lot of training for the TTT to play ideal moves. Even with 100,000 training sessions I found that I could beat it pretty easily with me playing optimized moves. Around 400,000 I saw a lot of improvement where ties became consistent. I ran into a small issue where my Jupyter notebook started becoming unresponsive past 400,000 sessions. During training I would go for about 400,000 sessions, and then do a warm start from that point because I saved all the moves, and then I did another two sets of 400,000. At this point I was getting the optimized moves and recieved draws every time unless I made a mistake and lost. A sample game takes place below.
Loading...
| |
| |
_____|_____|_____
| |
| |
_____|_____|_____
| |
| |
| |
Player 1 (X): 3
| |
| | X
_____|_____|_____
| |
| |
_____|_____|_____
| |
| |
| |
Player 2 (O): 5
| |
| | X
_____|_____|_____
| |
| O |
_____|_____|_____
| |
| |
| |
Player 1 (X): 1
| |
X | | X
_____|_____|_____
| |
| O |
_____|_____|_____
| |
| |
| |
Player 2 (O): 2
| |
X | O | X
_____|_____|_____
| |
| O |
_____|_____|_____
| |
| |
| |
Player 1 (X): 8
| |
X | O | X
_____|_____|_____
| |
| O |
_____|_____|_____
| |
| X |
| |
Player 2 (O): 6
| |
X | O | X
_____|_____|_____
| |
| O | O
_____|_____|_____
| |
| X |
| |
Player 1 (X): 4
| |
X | O | X
_____|_____|_____
| |
X | O | O
_____|_____|_____
| |
| X |
| |
Player 2 (O): 7
| |
X | O | X
_____|_____|_____
| |
X | O | O
_____|_____|_____
| |
O | X |
| |
Player 1 (X): 9
| |
X | O | X
_____|_____|_____
| |
X | O | O
_____|_____|_____
| |
O | X | X
| |
Winner: tie